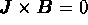再び電磁現象

縦磁界下での磁束分布は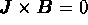のforce-freeモデルによってよく記述さ れることが経験的に知られている。このときの量子磁束の運動を 連続の式

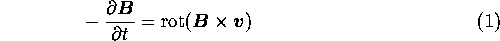
から調べると、回転運動が起こることが導かれる。こうした回転運 動が生じる根拠としてforce-freeモーメントが挙げられる。 (1)式とMaxwell方程式

を比較すると、一般に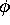をスカラー関数として

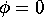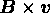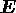の関係が得られる。通常の横磁界下ではとなって Josephsonの式となるが、縦磁界下でははゼロではない。こ のことは図2(c)の場合の量子磁束の回転運動を考えればよく分かる。 すなわち容易に示せるようには回転面に垂直なベクトルであり、回転中 心からの距離とともに大きくなるのに対して、は回転面内にあり、一様である。このことはエネルギーの 流れ(Poyntingベクトル)の方向が回転の侵入の方向と同じで、した がって回転そのものの方向とは垂直であることと関係している。す なわちこの場合の量子磁束の速度は位相速度と同じ意味しかもたない。 図1の抵抗状態における負の電界は(3)式の第１項から導かれるが [5]、 この項は広い面積で積分すればゼロとなり、エネルギー散逸に関係 した重要な項は第2項の方である。図1の結果は部分的にエネルギー 生成が行われているような錯覚を与えるが、実際には電流も円柱状 試料をらせん状に流れており、常に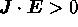となっているのである。

このように縦磁界下での超伝導体の電磁現象はforce-freeモーメン トにより駆動される量子磁束の運動に起因するものとして統一的に説 明することができる。