球殻の内側での電界について

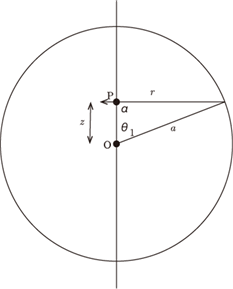
半径aの球殻表面に面電荷σが一様に分布している。
中心Oからｚだけ離れたz軸上の点Pにおける電界の強さを求めてみる。
結果はガウスの法則からも分かるよう球の外では電界はあるが、球内ではゼロになる。これをクーロンの法則からも確かめてみる。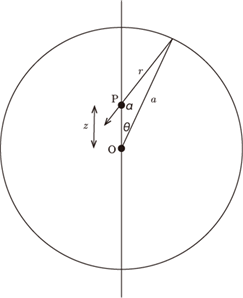

クーロンの法則による標式

図のように座標をとると、球殻の一部dθdφではσdθdφの電荷がある。それが点Pに及ぼす電界の強さは、向きの補正cosαを含めて、球殻の一部から点Pまでの距離rを余弦定理を用いて=というように求めて、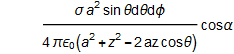

となる。これを方位角φについて0から2πで積分すれば、2πがかけ算されて、

となる。簡単のために=1として考えて、残りの積分を考える。ここで正弦定理を使えば
           cosα=cos(())
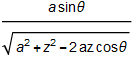となる。

積分でもとめる

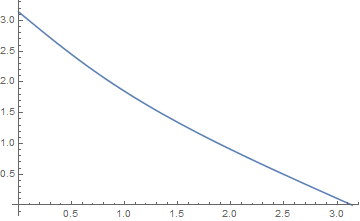
θが0から=ArcCos[z/a]の間では、αがπからπ/2に変化する。ここでの積分を行う。θ=の時にα=π/2である。また仮定としてa>0, z>0, a>zをつかう。結果はマイナスになり、z軸の負の向きにできている。

さらに、θがかπのあいだでは、αはπ/2から0と変化して、積分結果はプラスになる。この大きさが丁度さきほどの積分結果と同じになっている。

したがって、これらを足せば丁度0となる。このように球殻の内部では電界はゼロとなる。
言い換えると、zより大きいところの電荷の寄与と、zより小さいところでの電荷の寄与がちょうどつりあっており、電荷の大きさはゼロになる。

説明は次の図のとおり。θ=の時にα=π/2である。

数値積分の場合

次に数値積積分について検討する。
最初に、下記の様にθを0-> pi/2とPi/2->Piの二つの領域で計算するのは間違いである。正しくは、で分割する必要がある。ここでは、π/2でやってみる例を示してみる。

一応、0-> Pi/2 , Pi/2-> Piの積分値はちょうど逆になっているように見えるので、合計すればゼロとなっている。
しかしこれはzが小さくtheta1が90度に近かったからである。

たとえばa->10, z->3ではうまくいかない。

これは積分範囲が正しくなかったためで、次にtheta1を考慮すると次の様になり、プラスマイナスはちょうど同じになり、うまくいく。

θとαの関係

θが0から(α=π/2になるところ)と、からπまでと分けることができる。

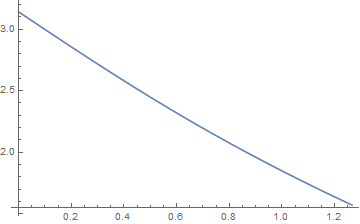
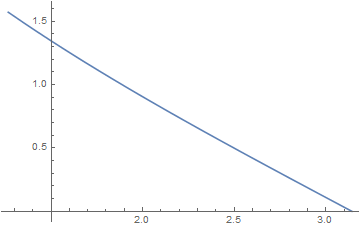
合わせて表示させれば下記の様になる。