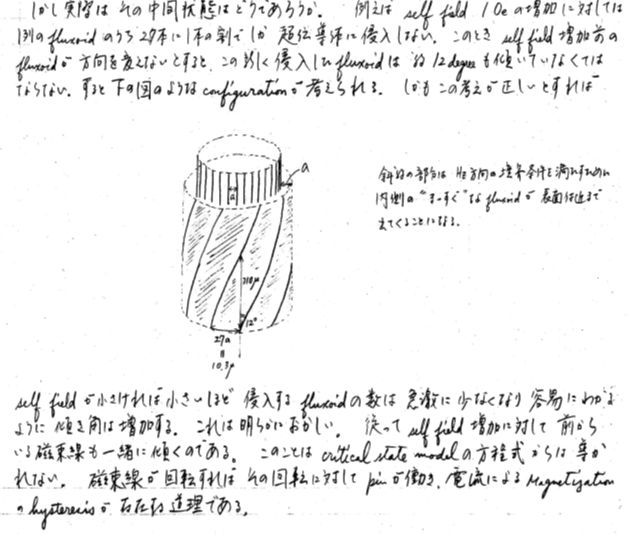
図1. 縦磁界中にある超伝導円柱への磁束の侵入を議論したときのメモ

(2) Force-free トルクの導出

　磁束と電流が平行であるforce-free状態においてはLorentz力は働かないが、磁束には図2に示したような扇を開いたような回転剪断歪が生じており、矢印で示したようにこの歪を減ずるようなforce-freeトルクが働くことを初めて明らかにした[2]。方法は仮想的にforce-free歪を導入したときのエネルギー上昇をMaxwell理論によって求め、この磁束の回転角に関する変化率から求めた。同様な方法によりLorentz力を導出することもできる。 　これにより、縦磁界下における臨界状態はforce-freeトルクとピンニングトルクとの釣り合いによって決まることになり、臨界電流密度がピンニングの強さに依存する実験結果[3,4]を説明することができる。なお、このトルクはLorentz力がないにもかかわらず存在する。すなわち、力のモーメントではなく、この点はトルクが力を起源とする力学と一線を画すものである。

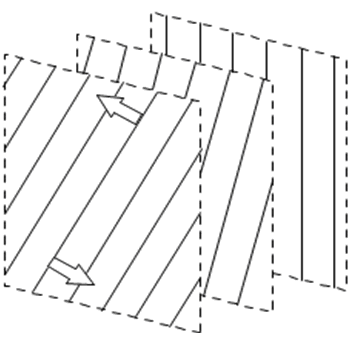
図2. Force-free歪

(3) Josephsonの理論において仮定されたゲージが正しくないことを証明

　Josephsonはピンがない場合の磁束の平衡状態はforce-free状態であるとして、この状態が安定であることを示した[5]。しかしながら、実際にはピンニングなしには磁束のforce-free状態は安定ではない。ここでは、force-free状態下での磁束の運動に対してJosephsonが仮定したゲージが正しくなく、正しいゲージを用いた場合、ピンがない超伝導体の電流密度は0でなければならないことを明らかにした。これはforce-free状態では磁束にforce-freeトルクが働くこととコンシステントである。

(4) 磁束の連続の式による磁束線の回転の解の導出

　縦磁界下で電流を流すようなforce-free状態が保たれた変動過程における磁束の速度を磁束の連続の式から求めた結果、磁束の回転の解が得られた[6]。この磁束の運動はトルクの釣り合いでピンニングトルクを上回ったforce-freeトルクにとって駆動されたものと見ることができることを明らかにした。

(5) 磁束の回転運動と誘導電界の関連

　磁束の回転運動が生じるとき、誘導電界がJosephsonの式（E = B×v ）から外れることを示した[6]。とくに、回転角度が小さい場合、誘導電界は磁束密度にほぼ平行となり、Caveらの実験結果に近い結果となることを示した。ここでは回転面内での運動の非一様性と電界の一様性の両立が可能であることを示した。また、この場合の誘導電界はE =-∂A/∂t = B×v - gradφの形（これを拡張されたJosephsonの式と呼ぶ）で与えられるが、第二項のφは静電位ではなく、この電界成分中に損失に関した重要な部分が含まれることを示した[7]。

(6) 臨界電流密度のピンニングトルク依存性

　常伝導析出物をピンにもつ超伝導体に対して、図3のように臨界電流密度がピンニングトルクに比例することを初めて実験的に明らかにし、force-freeトルクとピンニングトルクの釣り合いにより臨界電流密度が決まるという機構が正しいことを証明した[8]。なお、この超伝導体では横磁界下の臨界電流密度はN_pf_pに比例することが知られている。

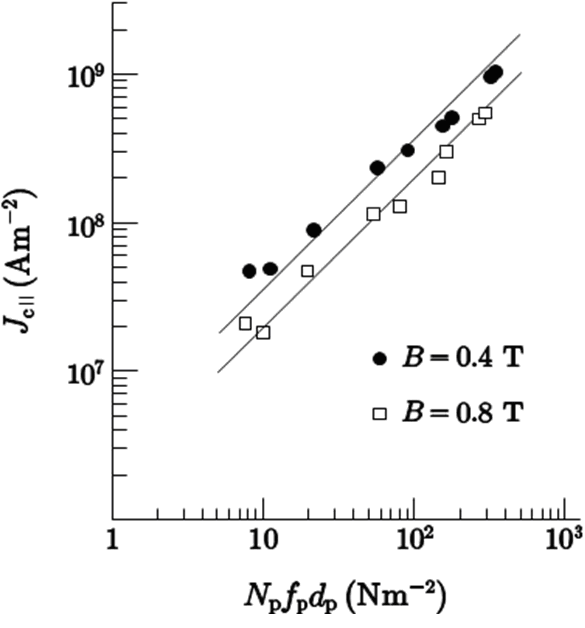
図3. 臨界電流密度とピンニングトルクとの関係（N_pとf_pはそれぞれBi析出物の数密度、d_pはその間隔）。図中、直線は理論予想を示す。

(7) 一般化臨界状態モデルの提案

　縦磁界下における磁束系の臨界状態を決定するのはLorentz力とピン力の釣り合いと、force-freeトルクとピンニングトルクの釣り合いである。両方の釣り合いにピンニングが関与し、そのピンニング・エネルギーが分配されることになる。したがって、ピンニング・エネルギーの分配の仕方が問題となるが、これがエネルギー散逸を極小にするように行われるという不可逆熱力学で広く一般に知られた法則を適用した。これに基づき二つの釣り合いからなる一般化臨界状態モデルを提出した[9]( エネルギー散逸極小の原理の応用を参照)。

　縦磁界下で電流を流すときなど、一般にforce-freeモデルが成立することが知られている。このように、ピンニングが有効に働いているにもかかわらず、ピン力の影響が現れないことを上の一般化臨界状態モデルで説明した。すなわち、ピンニングによるエネルギー損失は臨界電流密度の逆数に比例するが、縦磁界下の方が臨界電流密度が大きいことから、ピンニング・エネルギーは対応するトルクの釣り合いに重点的に分配されることになる。このため、ピンニング・エネルギーは力の釣り合いには分配されず、ピン力が現れることがない。こうしてforce-freeモデルが成立することが説明される。

　図4は超伝導平板表面の磁界角度を一定に保つように縦磁界と電流を同時掃引したときの臨界電流密度で、電流の流れ方に自由度を与えているが、電流は損失が少ないforce-free状態を構成するように流れ、通常の縦磁界下の臨界電流密度に一致している。この結果は上記のピンニング・エネルギーの分配の仕方により説明される[10]。

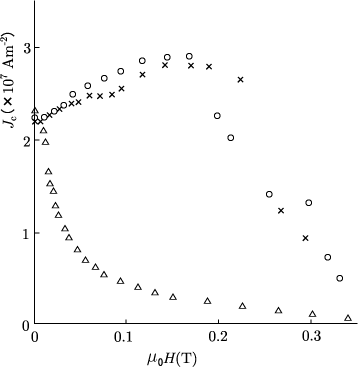
図4. 超伝導平板表面の磁界角度を一定に保つように縦磁界と電流を同時掃引したときの臨界電流密度。○は通常の縦磁界下、×は同時掃引時、△は横磁界下の臨界電流密度。

(8) 抵抗状態における負の電界構造の解明

　縦磁界下でも臨界電流密度以上の電流を流した場合、磁束が不安定となって運動を起こすと考えられる。この運動はピンニングトルクを上回ったforce-freeトルクによる回転運動であると考えられるが、そのままでは外部磁界と電流の自己磁界で決まった境界条件を満たさない。このため、定常的な運動とするために、磁束の併進運動が誘発されると考えられる。すなわち、図2の最も手前の列の磁束が矢印のように回転する場合、定常的な流れとなるためには、次の磁束列の位置にまで進む必要がある。超伝導円柱の場合にはこうした回転と併進により、図5に示したらせん磁束フローが起こると予想される[11]。すなわち、この場合も「円柱状の対称性からの破れ」が生じる。このとき、ピンニング・エネルギーはトルクの釣り合いに分配されているため、磁束にはピン力が働かず、したがって、併進運動によるエネルギー損失は起こらない。この場合も磁束運動で生じる誘導電界は拡張されたJosephsonの式となるが、損失成分は再び第二項- gradφに含まれる。実際に第1項はらせん構造の1周期で長さ方向に平均すると0となる。したがって、第2項に含まれる損失成分はforce-freeトルクに基づく回転運動から生じるもので、このピンニング損失を計算して表面電位を求めた。その結果が図6(a)で[11], Ezakiらの図6(b)の実験結果を説明する。ここで、負の電界は磁束が超伝導体の外部に出る部位において、電界の第1成分から生じる。したがって、負の電界領域においてもエネルギー生成のような特異なことは起こっていない。実際にJ・E > 0となっている[11]。

　また、この抵抗状態の抵抗率を求めると、Bardeen-Stephenモデルに従って縦磁界に比例しており、上記の理論結果に定性的に一致する[12]。この結果より縦磁界成分が一緒に運動するというらせん磁束フローが起こっていることが証明される。なお、磁束カッティングが起こるのであれば、発生するエネルギー損失はカッティング部分だけに限られることから、ひじょうに小さくなる。したがって、この結果は磁束カッティングが起こっていないことの直接の証明となる。

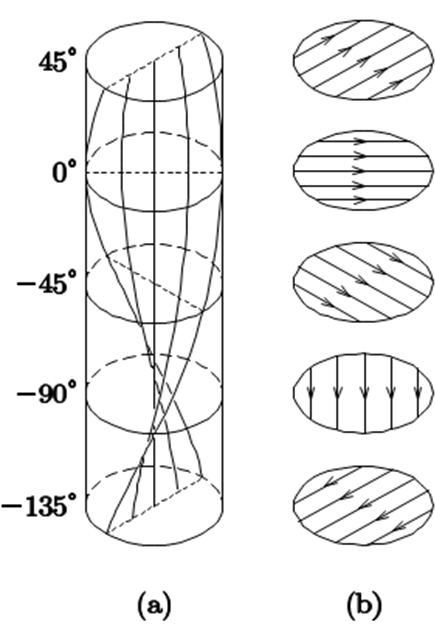
図5. らせん磁束フローモデル。(a)が中心軸を通る磁束の運動の様子を、(b)が長さ方向の各位置における運動方向を示す。

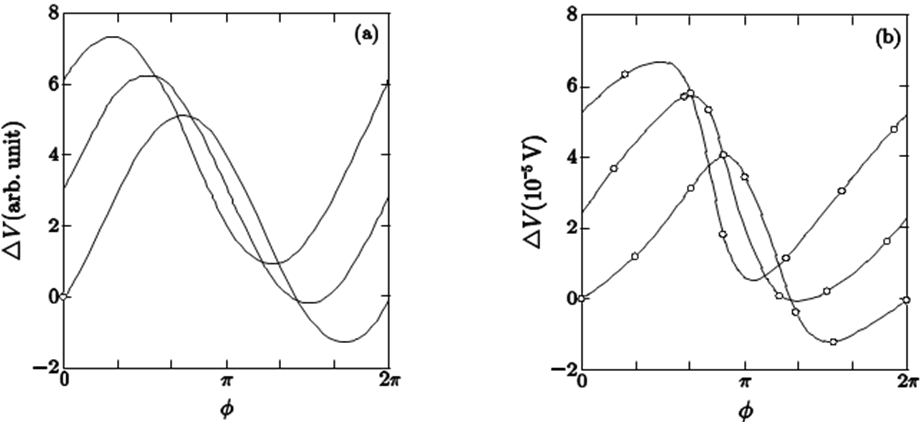
図6. 各長さ方向の位置における表面電位の方位角依存性。(a)が理論結果で(b)がEzakiらの実験結果。

(9) 横磁界下の電磁現象と縦磁界下の電磁現象の対応の明確化

　横磁界下では電流によって図7のような磁束の密度勾配や曲げが起こり、これらをなくすように磁束に磁気圧や線張力が働く。これらの駆動力がLorentz力である。そして、この力とピン力がつり合って準安定状態が形成される。したがって臨界電流密度はピン力で決定される。そして電流が臨界値を超えれば、ピン力を上回ったLorentz力によって磁束フローが起こり、電圧の発生や損失が起こる。

　一方、縦磁界下では電流によって磁束の回転剪断歪が生じ、これをなくすように磁束にforce-freeトルクが働く。そしてこのトルクとピンニングトルクがつり合って準安定状態が形成され、臨界電流密度はピンニングトルクで決定される。そして電流が臨界値を超えれば、ピンニングトルクを上回ったforce-freeトルクによって磁束の回転運動が生じ、電圧の発生が起こる。

　このように形式的には二つの現象は対応するが、結果としての電磁現象は大きく異なる[13]。すなわち、横磁界下では電磁現象は力学系の運動と類似するが、縦磁界下の回転運動に対してはそうした類似性は成立しない。このことはforce-freeトルクがLorentz力を含め、いかなる力をも起源としていないという力学系との相違に関係する。

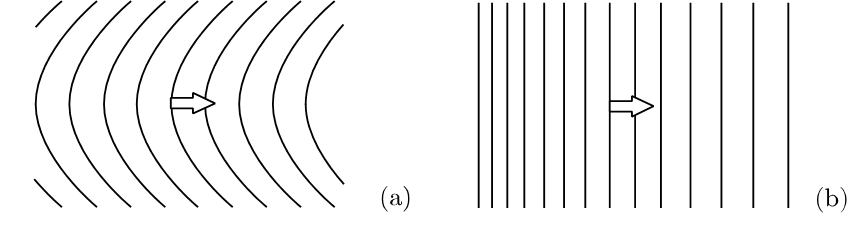
図7. 磁束の(a)密度差と(b)曲げ歪。これらの歪を減ずるように弾性復元力として矢印のようにLorentz力が働く。(a)の場合を磁気圧、(b)の場合を線張力という。

(10) 縦磁界効果の電磁気学的意義付け

　縦磁界効果の特殊な電磁現象をもたらすものは図2に示す磁束の歪を開放するforce-freeトルクであり、これはLorentz力など、他の電磁気学の原理とは独立な原理であり、これまでの電磁気学の中では知られていなかった原理である。このトルクの出現は超伝導体では電気抵抗がないため、図2のような電流の流れ方が可能であることに起因する。通常の、Ohmの法則が成立する場合、電流は最短路を直線的に流れ、図2のような電流の流れは実現しないからである。こうした電磁気学の体系を図8に示す。なお、Coulombの法則はCoulomb力に、Bio-Savartの法則はLorentz力に含まれるとする。また、この中で、唯一、Ohmの法則が理論的に証明がされていない経験則であり、かつエネルギー散逸に関係しているという特殊なものである。

　超伝導体ではOhmの法則が成立せず、電流の流れ方は関係するエネルギーの最小原理という純粋物理学的な機構で決まり（ピンニングの加算理論の項参照）、その意味でより純粋な系である。超伝導現象は特殊と考えられがちであるが、大部分の元素やほとんどの金属化合物が超伝導を示すことや、初等電磁気学の枠組みの中に超伝導現象がそのまま組み込まれる（電磁気学の項参照）ことを考えれば、図8に示される体系は一般的なものといえよう[13]。

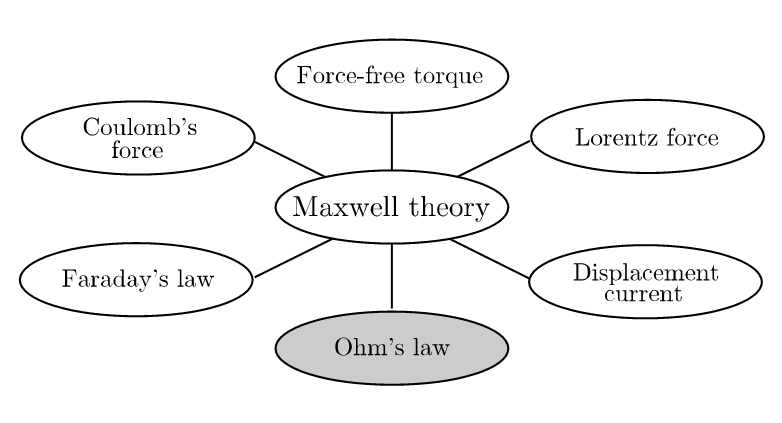
図8. 超伝導を含む電磁気学の体系

最後に、縦磁界効果に関する文献としては主要研究論文の[1]、[13]、[14]を参照されたい。